If you have studied any engineering career, you should have studied at some point numeric analysis and learned the least-squares method. Just remembering you, the least-squares method aims to minimize the error of the given points when guessing the curve coefficients.
So, if you have some points and you know the order of the equation, this is what you need to know to get the coefficients.
I will write in this article how I used a PHP Artificial Intelligence library to solve any N-order linear equation.
The Machine Learning Library for PHP
I must say this PHP library is more than awesome, it implements many Artificial Intelligence algorithms, but for now, I will focus on least-squares.
You must have PHP 7 to use this library, also there is not an easy way to install it without the composer. The GitHub project website explains very well the installation process. So, I will skip it.
The Third-Grade Equation Experiment
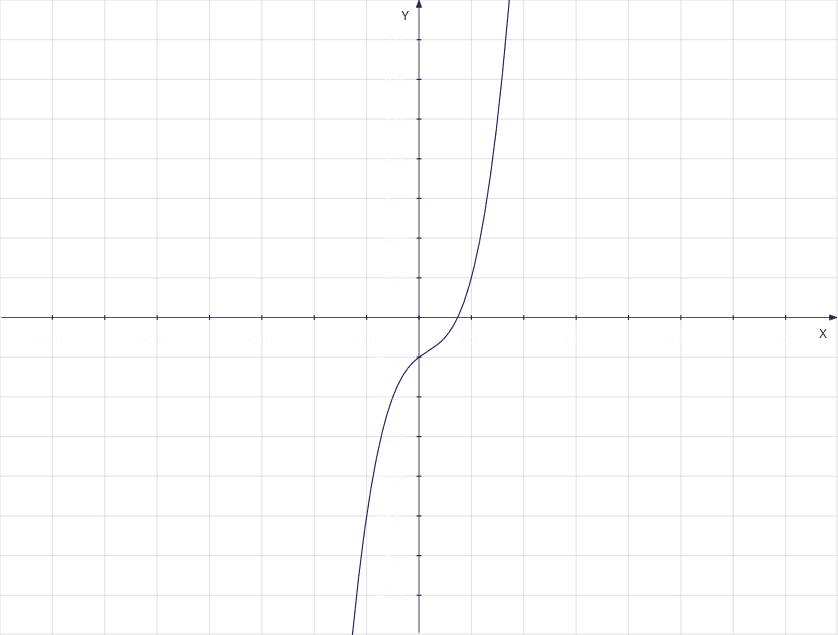
I selected the following equation as a test subject: f(x) = 2x3−x2+x−1. The following graph is the result of this equation.
| x | f(x) |
| -4 | -149 |
| -3 | -67 |
| -2 | -23 |
| -1 | -5 |
| 0 | -1 |
| 1 | 1 |
| 2 | 13 |
| 3 | 47 |
| 4 | 115 |
Coding in PHP
Here is the code I am using. It is quite simple.
include 'vendor/autoload.php';
use Phpml\Regression\LeastSquares;
$samples = [[-64,16,-4], [-27,9,-3], [-8,4,-2], [-1,1,-1], [0,0,0], [1,1,1], [8,4,2], [27,9,3], [64,16,4]];
$targets = [-148, -65, -24, -5, -2, 1, 14, 45, 117];
$regression = new LeastSquares();
$regression->train($samples, $targets);
print_r ($regression->getCoefficients());
print_r ($regression->getIntercept());
echo "\n";
echo $regression->predict([125,25,5]);
echo "\n";
Since the f(x) = Ax3 + Bx2 + Cx + D form, the $sample array contains the values of x3, x2 and x. The $target array contains the values of f(x). Remember that the problem here is we do not know A, B, C and D; we only have some points and we know the order of the equation.
Please note that the $targets array is having results with errors. I put these errors on purpose.
Executing the Code and Comparing the Equation
I got the following output:
Array
(
[0] => 2.013468013468
[1] => -0.88744588744589
[2] => 0.7744107744108
)
-1.5281385281385
231.84126984127
Which it means g(x) = 2.013468013468 x3 - 0.88744588744589 x2 + 0.7744107744108 x - 1.5281385281385.
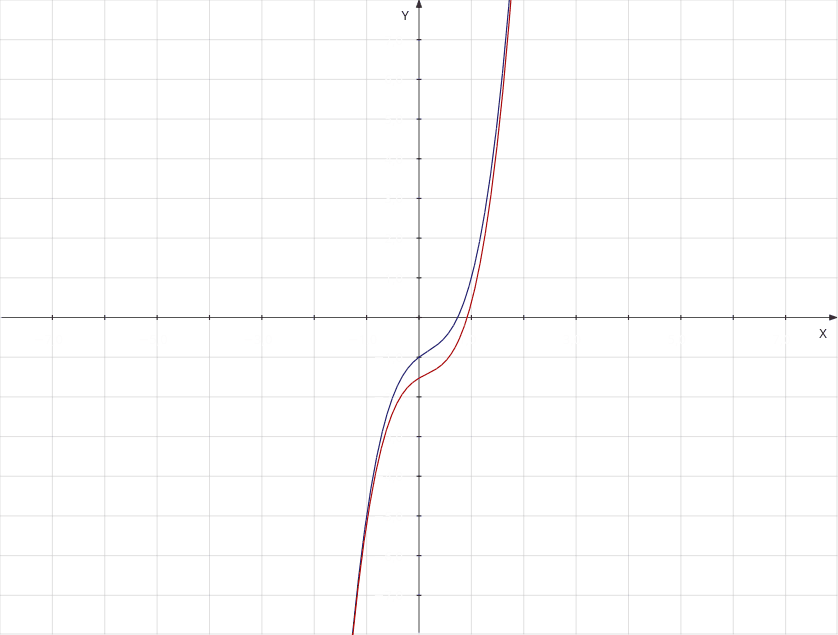
Let's evaluate against 5, f(5) = 229 and g(5) = 231.84126984127 which is pretty close. Look at the following graph, f(x) in blue, and g(x) in red.